凝聚态物理主要研究什么?凝聚态物理就业前景
凝聚态物理是研究物质的宏观集体行为及其与微观相互作用的学科。它研究物质的固态和液态性质,重点关注物质的结构、热、电、磁、光等性质在凝聚态下的表现形式和规律,探究物质的微观性质与宏观物理行为之间的关系。凝聚态物理的研究范围广泛,从单个原子、分子到固体、液体、气体、等离子态,包括超导、超流、量子力学效应等,都是凝聚态物理的研究内容。以此为基础,凝聚态物理为当代科技发展奠定了重要基础,例如,在半导体物理的研究中提高了晶体管、太阳能电池等的效率,促进了信息技术与能源技术的发展。
一:凝聚态物理主要研究什么
凝聚态物理学是研究凝聚态物质的物理性质与微观结构以及它们之间的关系,即通过研究构成凝聚态物质的电子、离子、原子及分子的运动形态和规律,从而认识其物理性质的学科。
一方面,它是固体物理学的向外延拓,使研究对象除固体物质以外,还包括许多液态物质,诸如液氦、熔盐、液态金属,以及液晶、乳胶与聚合物等,甚至某些特殊的气态物质,如经玻色-爱因斯坦凝聚的玻色气体和量子简并的费米气体。
另一方面,它也引入了新的概念体系,既有利于处理传统固体物理遗留的许多疑难问题,也便于推广应用到一些比常规固体更加复杂的物质。
起源发展:
凝聚态物理学起源于19世纪固体物理学和低温物理学的发展。19世纪,人们对晶体的认识逐渐深入。1840年法国物理学家A·布拉维导出了三维晶体的所有14种排列方式,即布拉维点阵。
1912年,德国物理学家冯·劳厄发现了X射线在晶体上的衍射,开创了固体物理学的新时代,从此,人们可以通过X射线的衍射条纹研究晶体的微观结构。
19世纪,英国著名物理学家法拉第在低温下液化了大部分当时已知的气体。1908年,荷兰物理学家H·昂内斯将最后一种难以液化的气体氦气液化,创造了人造低温的新纪录-269 °C(4K),并且发现了金属在低温下的超导现象。
超导具有广阔的应用前景,超导的理论和实验研究在20世纪获得了长足进展,临界转变温度最高纪录不断刷新,超导研究已经成为凝聚态物理学中最热门的领域之一。
二:凝聚态物理就业前景
就业前景还是很好的。凝聚态物理学是从微观角度出发,研究由大量粒子组成的凝聚态物质的结构、动力学过程及其与宏观物理性质之间联系的一门学科。国内有很多知名的科技企业都在做相关研发,如华为等。
三:凝聚态物理研究生大学排名
以固体物理为主干的凝聚态物理,通过半个世纪的迅速发展,已经成为当今物理学中的最重要的分支学科之一。根据国外的统计,发表的物理学的论文中约有三分之一属于凝聚态物理;而物理学工
01周期结构、破缺的平移对称性
固体物理的一个根本出发点在于考虑所谓破缺的对称性(broken symmetry)。这个名称是朗道在讨论相变问题时首先提出的[1]。我们知道,在一般情形下,空间是均匀的,而且是各向同性的;基本粒子所遵循的规律也具有高度的对称性。至于介质,气体与液体的对称性也是非常高的,对于任意的平移和旋转均具有不变性;唯独固体的对称性是不完全的,这种破缺的对称性成为固体的一个最重要的特征。固体物理的基本任务在于要从微观上理解固体的各种性质,阐明其规律性。因此,如果要从历史上追溯固体物理的起源,那么,就应该探究一下科学家从什么时候起,开始考虑固体破缺的平移对称性。我对于科学史没有进行过专门的研究,因此只能提出一些不成熟的个人看法。如果要为固体物理找一位始祖的话,我认为,开普勒将是一位合适的候选人。开普勒的行星运动三定律是众所周知的,但不甚为人们所知晓的是他在1611年写过一篇题为《论六角雪花》的文章,讨论雪花的对称性[2]。大家都知道,雪花具有六重对称性,和液体相比,这是一种破缺的旋转对称性。开普勒的文章中认为雪花的六重对称性可能是微粒作周期性排列(即破缺的平移对称性)的结果。他首先考虑两种平面上球体排列的模型∶一是具有四重对称性;另一是具有六重对称性,后者为平面密排。他还进一步探讨了不同层序的堆垛∶一是从四重对称性的平面排列出发,逐层具有相同的排列,都对准原来球体的位置。这样,就构成了简立方结构;另一是从六重对称性的平面排列出发,上面一层堆在下面一层的间隙位置,从而形成密堆结构。这篇文章给出了一个重要的线索,即观测到的晶体的宏观对称性是以构成晶体的粒子排列的微观对称性为基础的。很显然,微观对称性的特征在于破缺的平移对称性,只对于一组离散的平移矢量具有不变性,给出了晶格概念的雏形。
十八世纪末,R. J. Hauy就在天然矿物晶体测角术的基础上,建立了几何晶体学的基本规律。到十九世纪中,Hassel推导出32种点群,布喇菲推导出14种点阵;到十九世纪末,Fedorov与熊夫烈分别独立地推导出230种空间群,从而全面奠定晶体微观对称性理论的基础。这个理论影响深远,构成了固体理论的第一根柱石。讨论对称性问题的科学语言是数学上的群论。群论的应用可以使得许多固体理论的计算得到简化。
固体物理发展史中的一个重要里程碑,就是1912年劳厄等发现X射线通过晶体的衍射现象[3]。当时劳厄在慕尼黑大学任教,而厄瓦耳则为该校理论物理教授索末菲的研究生。厄瓦耳正在做博士论文,课题是对于晶体的双折射现象进行微观的理论解释。当时量子力学尚未问世。因而是在洛伦兹的经典色散理论的范围内进行的。厄瓦耳设想晶体中的偶极子按点阵排列,在入射电磁波作用下,形成的振动偶极子阵列,发射次级电磁波。他在做论文过程中曾向劳厄求教,劳厄反过来问他的偶极子阵列的间距大致多少厄瓦耳估算了一下,认为是10-8厘米的量级,正好是X射线波长的量级(虽则X射线是否是电磁波,当时尚有争议)。
劳厄当时正好应数学百科全书的邀请,写了一篇关于物理光学的总结,其中他将一维光栅的衍射理论向二维作了推广。这样,晶体就相当于天然的三维光栅,对应的衍射理论可以从二维推广到三维。于是找了索末菲另外的研究生帮他做实验。经过一段时间摸索后,终于照出来了 *** 铜的衍射斑点,并且作出了正确的理论解释。随后W. H. 布喇格与W. L. 布喇格测定了NaCl与KCl等晶体的结构,揭开了晶体结构分析的序幕。在两次世界大战之间,晶体结构分析的理论和实践都有了很大的进展,使得固体具有周期性结构的概念深入人心,为固体物理学的发展铺平了道路。二十年代后期发现电子衍射术,二次大战后,又发现了中子衍射术,为结构分析扩大了研究手段。七十年代以后,高分辨电子显微镜点阵成像技术的发展,使得晶体结构的直接观察成为可能。值得一提的是,这样就可以直接观察到局域内结构的差异,不像通常衍射 *** 所求出的是平均结构。
如果说二十年代是原子物理的黄金时代,那么,三十和四十年代乃是核物理的黄金时代。当时,固体物理只是一般很不显眼的潜流。记得我在四十年代念大学的时候,就从来没有听说过固体物理这一学科的名称。当时翻开《物理评论》这一类典型的物理杂志,其中登载的几乎是清一色的核物理的文章,其他方面的工作寥寥无几,难与其抗衡。但到二次大战结束以后,固体物理的蓬勃发展才开始为人注目。在这个转折过程中,W. L. 布喇格在剑桥大学卡文迪什实验室的工作,在物理学的发展史上留下了印痕。三十年代末,卢瑟福去世,布喇格继任卡文迪什物理学教授。这是一个举足轻重的职位。因为剑桥大学该实验室有极其光荣的传统,历任教授及其指导的许多学生都对物理学发展有杰出的贡献。可以毫不夸张地说,半部近代物理学史是在这个实验室里写成的。特别是在卢瑟福任职的年代,人才辈出,成果累累,成为世界核物理(也就是当时的高能物理)研究的中心。在布喇格继任以后,有人问他有何打算?他说,英国已经教会了人家如何进行核物理的工作,今后要做一些别的方面的工作。他不顾当时英国物理学界的反对,对核物理不予重视。他转而搞晶体结构分析,大胆扶植了关于蛋白质结构和DNA结构的研究。与此同时,也支持M. Ryle利用第二次世界大战废弃的雷达设备,建立了射电望远镜。他为开创分子生物学和射电天文学这两门边缘学科作出了贡献,而卢瑟福建立起来的强有力的核物理班子就遽然星散。有名的理论物理学家F. Dyson在四十年代的剑桥做过研究生。他对当时的所见所闻,困惑不解。M. Perutz 宣称,他为搞清楚马肌红蛋白的晶体结构已经花费了十年工夫了如果再给他十五年的时间,也许能够拿下来。又有F. Crick尽是一些怪想法,毫不沾物理的边。Dyson感到在剑桥学不到物理学了,于是离开剑桥去美国的普林斯顿。后来他在那里以量子电动力学重整化问题的出色工作而闻名于世。Dyson在七十年代初写了一篇题为《物理学的未来》的文章[4]。他回顾说,当时英国物理学界都在咒骂布喇格,说他损坏了卡文迪什的光荣传统,他也有同感。但是事隔三十年后,他对这个问题进行了重新估价。不能不承认布喇格进行变革所取得的巨大的成功,对于布喇格的勇气和远见表示钦佩。事实上,从当时的情况来看,英国继续在核物理领域进行竞争的话,也不可能保持领先的地位。因为经济条件决定英国无法和美国进行加速器的竞赛。即使卢瑟福不死,也不可能阻止高能物理中心从剑桥转移到美国的柏克莱。但是由于布喇格的卓识,剑桥却在两个新兴领域居世界领先地位,获得一连串的诺贝尔奖(其中许多是化学和医学奖)。特别值得称道的是Watson与Crick确定DNA双螺旋结构的工作,由碱基配对的序列作为遗传密码,不仅在分子生物学上有划时代的意义,也是二十世纪最重大的科学成果之一。它显示出凝聚态物理在边缘学科方面具有的强大生命力。还应该指出,正是广义的晶体学研究(包括分辨率为原子尺度的常规结构分析和电子晶格像技术,分辨率为数十埃的电子衍衬像技术,以及分辨率更差一些的扫描电镜、光学显微镜及X射线形貌术等)构成了材料科学的基础。
固体具有周期性结构还有一个重要后果,牵涉到固体的“固”性,或称为刚度(rigidity)。因为周期性的原子排列,使得原子具有大致确定的位置。这种刚度也是和破缺的平移对称性相联系的。使固体的属性和流体迥然不同。P. W. 安德森很有风趣地解释了十八世纪英国Samuel Johnson 博士反驳贝克莱主教的主观唯心论的一段轶事[5]。Johnson踢一脚石头,由疼痛的感觉证实客观世界是存在的。安德森认为这是由于他踢的石头具有刚度,这是破缺平移对称性物体的属性之一。
02周期结构中波的传播
如果将固体物理比拟为声彩并茂的戏剧,那么,最主要的剧目就是周期结构中波的传播。这里所说的波范围甚广,包括弹性波、电磁波与德布罗意波等。对于固体理论有重要贡献的布里渊于1946年曾经出版了一本题为《周期结构中波的传播》的小书[6],强调了各种波在周期结构传播的共性,触类旁通,很有启发性。关于周期结构中波的传播这一问题的理论探讨,也是由来已久。一维周期链上弹性波的传播,可以追溯到牛顿在《自然哲学的数学原理》中对声速公式的推导。当时还没有偏微分方程,牛顿只得借助于一维晶格模型来进行计算。十八世纪中伯努利父子探讨了一维晶格的本征振动频率的问题。十九世纪中,科希、Baden-Powell与开耳芬等相继地采用一维晶格的机械振动模型来处理光的色散问题,获得了带通频段与截止频率等重要概念。二十世纪初坎贝耳将这些概念应用到发展电磁滤波器这一技术问题上去。1912年玻恩与卡曼处理了三维晶格振动问题,为随后玻恩学派系统地发展晶格动力学理论奠定了基础。晶格动力学是继晶体对称性理论之后较早发展起来的一个固体理论领域。早年的工作中,原子相互间作用采用了经典的有心力近似的假定;以后摒弃了这些限制性的假定,将理论建立在更普遍性的量子力学绝热近似的基础上。这方面的工作总结在玻恩与黄昆合著的《晶格动力学理论》这一经典性的专著之中[7]。晶格动力学理论曾用于解释一系列的晶体的热学性质、弹性性质、介电性质和光学性质。晶格动力学的实验检验开始于X射线的漫散射和晶体红外光谱的研究,到六十年代以后,中子非弹性散射与激光非弹性散射又为探测晶格振动的模式和测定其色散关系作出了重要贡献,使得晶格动力学理论的许多推论得到实验的证实。
至于晶体中电磁波的传播问题,由于周期结构的间距要比可见光波长小得多,所以通常的晶体光学问题不需要考虑周期结构的影响,虽然前面提到厄瓦耳曾经考虑过周期结构对光双折射的影响。在X射线被晶体衍射现象发现以后,X射线在周期结构中的传播问题就提到日程上来了。简单的衍射理论,忽略了入射束与衍射束的动力学相互作用,因而被称为运动学衍射理论。这种理论的缺点很明显,它不具有自洽性,也违背能量守恒定律。1914年C. G. 达尔文提出了考虑到透射束与反射束及多次反射束之间振幅消长的动力学衍射理论。不久厄瓦耳将他的光双折射理论发展为比较完备的X射线动力学理论[8]。理论处理是自洽的,各个被激发的偶极子所发射的次级电磁波的总和应等于原来入射的平面波。厄瓦耳发现入射波与衍射波之间存在振动式的能量交换,和耦合摆类似,称之为摆动解(pendellösung)。把晶体的衍射强度与衍射理论的计算结果进行对照,发现多数实际晶体内存在缺陷,使实测强度反而接近运动学理论估算的结果,以致 X射线动力学理论长期被人束之高阁。一直到五十年代以后,高度完整的人工晶体问世,观测缺陷的X射线衍射形貌术得到发展,方始重新为人们所重视。应该指出,厄瓦耳的动力学理论虽然深奥费解,但在数学处理上是很有特色的,对于晶体中其他的波的传布问题也产生影响,例如能带理论中的Korringa-Kohn-Rostoker(KKR) *** ,以及黄昆在发展玻恩的点阵动力学理论的普通形式,对之都有所借鉴。1928年Bethe简化了厄瓦耳的动力学衍射理论来处理电子衍射的问题,求解了周期势场中电子运动这一量子力学问题,接触到固体物理的一个核心问题。
早在十九世纪人们已经掌握了有关金属电导的基本经验规律(欧姆定律,电阻率与温度的关系等)。二十世纪初,Drude等企图用经典的电子理论来进行解释,遇到了不可逾越的困难。关键的问题在于无从理解金属为什么具有那么良好的导电性。因为晶体中原子的堆积极为紧密,原子的间距为埃的量级,而原子对电子散射的有效直径亦大约为埃的量级,这样电子在点阵中的运动将被原子多次散射,使得其平均自由程微不足道(埃的量级)。但是根据实测的金属电导率来推算,晶体中电子的平均自由程显然要大得多(100 埃以上)。如何来解释电子几乎不受阻碍地穿过完整晶体呢?德布罗意波的概念提供了解决问题的线索。二十年代中量子力学问世,首先在原子物理的领域取得了巨大的成功,进一步发展就分道扬镳∶一条道路通向原子核和基本粒子;另一条道路则进入分子结构和固体理论的领域。1927年,布洛赫去莱比锡大学海森伯处进修,海森伯当面提出了两个待解决的问题,一是金属导电的理论,另一是铁磁性的理论。布洛赫选择了前一课题,海森伯自己处理了后一课题。布洛赫近似地求解了周期势场中的薛定谔方程,数学上采用了经典的傅里叶展开法,物理图像的启发则来自一个普通物理演示实验——演示波的传布的一系列的耦合摆[9]。布洛赫得出了满足周期势场条件的布洛赫波函数,他的结果和Bethe的电子衍射动力学理论颇为相似,但他的注意力放在电子的能态上,探求波矢与能量之间的关系。在一般情形下,波矢与能量之间存在单值和连续的函数关系,对应于波能够无阻尼地透过晶体。而在对应于满足布喇格反射条件时,出现了能隙所对应的截止频段。因而波矢与能量的关系表现为一系列的能带,相邻能带间存在能隙。布洛赫所创建的能带理论,对于固体物理的发展产生了深远的影响。以周期势场为微扰的近自由电子近似,可对于一系列金属与合金的物理性质进行理论解释,这方面的成果总结在莫脱与琼斯的《金属与合金性质的理论》(1936)这一固体物理早期的专著之中[10]。
半导体早在十九世纪就已发现。有名的法拉第曾经注意到AgS具有负的温度系数,和一般金属正好相反。1931年A. H. 威尔逊首先用能带理论来解释半导体的导电现象——即能带填满而能隙较小,可以通过热激发使电子跃迁到空带上来进行导电[11]。这样,在半导体中载流子有两种类型,一是电子,一是带正荷的能带中的空穴。而且半导体的电导对于掺杂非常敏感,提供人为控制导电的可能性。值得注意,在无线电技术的初期,广泛应用的矿石检波器,实际上是一种半导体器件。但是由于性能不稳定,逐步为电子管所代替。到第二次世界大战时,由于雷达技术的发展,需要微波频段的响应良好的检波器,又将锗、硅这些元素半导体的研究提到日程上来了。终于在战后的1947年底,贝尔实验室的科学家巴丁、Brattain与肖克莱发明了晶体管[12],从而取得固体物理在应用上最重大的突破。
在晶体管的发明和发展之中,贝尔实验室扮演了关键性的角色,这绝不是偶然的[13]。贝尔实验室是以发展电信事业为目的的企业实验室,具有十分明确的应用背景。但是这个实验室的领导人具有远见卓识,对于一些被安德森称为“无穷大乘零”的基础研究,也给予重视和支持。“零”是指基础研究中有应用可能的几率几乎是零;而“无穷大”是指一旦成功,其收益可以说是无穷大。像晶体管的研究,贝尔实验室的花费不超过一百万美元,而产生亿万美元的新企业,改变了整个社会的生产面貌。早在四十年代初,贝尔实验室就成立了以肖克莱为首的固体理论小组,放手开展固体理论的基础研究;第二次世界大战后,又聘请了固体理论造诣甚深的巴丁来实验室工作,使得贝尔实验室在理论准备方面处于领先地位。另一方面,固体物理的研究是和材料制备方面的工作密切相关的。贝尔实验室动员了冶金学家和化学家参加半导体材料研制工作。首先制出了纯度较高多晶锗锭,获得了p-n结,为晶体管的问世创造了条件[12]。随后又大力发展了区域提纯和直拉法制备单晶外延生长等新技术,从而使锗和硅成为纯度最高、结晶完整性也最高、品质鉴定最清楚的固体材料。正如一张白纸,才能画出最新最美的图画。这样,固体物理学家的许多理论设想才可以在实验室中体现出来,不致为许多旁枝末节的因素所掩盖。半导体的发展,充分地证实了材料科学研究对固体科学发展的重要性。
布洛赫所提出能带理论的雏形,得到进一步发展,维格纳与赛兹进行了更认真的理论计算,对于碱金属的内聚力问题给出更加可靠的数据。随后多种计算方案,如正交平面波法、缀加平面波法、KKR *** 等相继提出。这些理论大多建立在哈特里-福克近似的基础上[14]。后来计算技术的发展使得人们可以较确切地计算许多材料的能带结构。六十年代以后,考虑到在多粒子相互作用的均匀电子气的能带 *** (如局域密度泛函理论等)也得到了发展[15]。由于计算技术的高度发展,对于较复杂结构晶体的能带的从头算起(ab initio)已经可能,也累积了许多实际材料的能带结构的资料。
平行于能带理论的发展,关于固体电子结构的实验研究也在广泛进行。早年有关能带结构的实验数据来自软 X射线谱,近年来已为更加精确的光电子能谱 *** 所取代。金属能带结构的特征在于有明确的费米面。从五十年代以后,利用de Hass-Van Alphben效应多种 *** ,发展了费米面探测技术,取得了不少结果。能带已经不仅是理论的构想,而且是在实验室中可以用许多 *** 来观测检验的实体。
科学的理论不仅可以帮助我们认识世界,更加重要的是可以改造世界。建立于周期势场中电子态的能带理论也引导科学家去设想超晶格的材料,在通常晶格周期上再加上一维超晶格周期,如果这个周期为几十埃的量级,比电子的平均自由程小,而比晶格周期要大,显然会影响电子的能态。Esaki等对此作了理论分析,发现超晶格将使能带分划为次带,具有高度非线性的色散关系。这样的能带结构将导致一系列特殊传输和光学性质等。分子束外延技术的发展,使得人工制备超晶格半导体材料成为可能,由于周期是可以人工控制的,就可以随心所欲地改变材料的物理性质[16]。除了两种成分不同晶体所构成的超晶格以外,掺杂作周期性调制的超晶格[17],容许对有效能隙和载流子浓度进行人工的控制,可以获得甚高的迁移率。这样,在超晶格材料的基础上正在发展具有特殊性能的电子学和激光器件。除了半导体超晶格以外,也发展了人工制备的金属超晶格[18]。金属超晶格的性能可以不同于构成它的两种组元,已经观测弹性模量的增强效应以及异常磁性与传输性能。可以预期,人工制备超晶格所涉及的材料、组合方式和物理效应的面还会继续扩大;而在基础理论和实用化器件上都可能出新的成果。总之,这方面的发展显示了凝聚态物理理论和实验结合的强大生命力,令人振奋地展示了运用基础理论来设计和发展新型材料和器件的美好前景。
03不同的基态
从单电子的能带理论出发,体系的基态,无非是电子按能级填充,直到费米面为止。这是忽略了相互作用体系的基态。实际上构成凝聚态的是大量粒子的体系,粒子之间存在相互作用,导致在一定条件下形成具有有序结构的基态。这种基态总是和某种对称性的自发破缺相联系的。在前面我们着重讨论了和平移对称性破缺相联系的晶格这一种基态,它对于固体的一系列性质产生深远的影响。虽然晶格作为基态从直观上来看是极其自然的,但应该指出,迄今为止,对此尚缺乏严格的论证。当然这也绝不是唯一的基态。可能存在各式各样的基态。它们对应于特定的对称性的破缺,例如对应于空间反演对称性破缺的铁电体与反铁电体,对应于时间反演对称性破缺的铁磁体与反铁磁体。
下面讨论有关磁有序结构的问题[19]。时间反演会引起电流的反向或磁矩的倒转。因而晶格座位上磁矩作有序排列必然破坏时间反演对称性。铁磁体是早为人类所熟知的,十九世纪末,居里等人就开始对其规律性进行了研究。二十世纪初,外斯引入了分子场的概念,建立了最早的铁磁性的理论,虽则对于分子场的物理本质并不理解。至于不具有宏观自发磁矩的反铁磁体,则要等到1932年方始为奈耳所发现。随后又发现了一系列磁矩作反平行排列但宏观自发磁矩不为零的亚铁磁体,技术中有重要应用的铁氧体就属于这一类。海森伯首先建立了以局域磁矩为基础的铁磁性量子理论∶相邻自旋Si与Sj的相互作用能可以表示为U= -2JSi·Sj,这里的J为交换积分,它和原子i与j的电荷重叠分布有关。如果J为正值,将导致铁磁性,若J为负值,则将导致反铁磁性。由于海森伯模型只考虑局域的自旋,主要适用于绝缘体磁有序材料。克喇末与安德森提出了通过氧离子耦合的超交换作用来解释一些氧化物的反铁磁性,成为铁氧体磁性材料的理论基础。
为了解释过渡金属的磁性,提出了巡游电子的物理图像,即认为d电子既和局域电子不同,又和自由电子不尽相同,它们是在各原子轨道上依次巡游,起主要作用的是在原子内部的电子间的交换相互作用。Stoner发展了相应的能带模型,可以解释过渡金属的磁矩为非整数的波尔磁子数,但不能很好地解释磁化率的居里-外斯定律。一个表面上看起来比较简单的问题是,在正常金属中溶有少量具有磁矩的杂质原子。安德森曾从理论上探讨了溶质原子保留其局域磁矩的条件。近藤以具有磁性的溶质原子在低温连续地转化为非磁性原子来解释有些合金电阻-温度曲线具有极小值的现象。这种近藤效应实际上是一个复杂的多体问题,曾得到许多理论物理学家的
另一类重要问题牵涉到规范对称性的破缺。粒子数守恒或电荷守恒体系的哈密顿量表现出规范对称性。此时场量将以ρ(r)=φ(r)·φ*(r)的形式关联于相互作用项,因而将φ(r)乘以任意的位相项eiη,而φ*(r)乘上e-iη,将使哈密顿量不变。规范对称性的实质就是波函数的位相具有任意性,不受约束。而规范对称性的破缺即表现为位相的相干性,因而可用宏观的波函数来描述这一类量子现象。超导就是一个突出的例证。早在1911年超导现象即为K. Onnes所发现,但长期以来,未能得到理论的解释,成为科学上有名的悬案[21]。布洛赫在回忆中讲到他成功地解释了正常电导以后,泡利就建议他接下来攻超导问题。结果事与愿违,泡利还颇有微辞。但他在工作中却证明了“有电流的状态不可能是基态”这一定理,从而否定了不少不成熟的超导理论,为正确理论的发展扫清了道路[8]。1933年发现了迈斯纳效应,从而确立超导态是作为一种热力学平衡态存在的。随后F. 伦敦正确地指出了超导是一种宏观量子现象,并给出了有关超导电动力学的正确的唯象描述。1950年京茨堡与朗道将超导的有效波函数作为体系的复序参量,采用自由能极小条件,导出了非线性的京茨堡-朗道方程,成功地描述了非均匀的超导体。作为唯象理论的重大成果而推广的这一方程,也在凝聚态物理的其他领域(如液晶、电荷密度波等)中发挥了重要作用。也正是在1950年H. Fröhlich提出了解决超导微观机制的一个重要线索,即认为金属中电子与晶格振动的耦合是超导的根源。接着实验工作证实了他预期的同位素效应,为这个设想提供有力的支持。方向虽然找到了,但理论的进展依然是缓慢的。因为这是一个复杂的多体问题,而当时的固体理论家一般还不熟悉量子场论的 *** 。有鉴于此,巴丁请杨振宁介绍一位熟悉这方面的粒子理论物理学家F. 库珀来做他的助手,并指导他的研究生J. R. 施里弗来攻这个难题。终于在1957年提出了有名的BCS理论[22]。认为电子与晶格振动的相互作用,使费米面附近的电子配对,从而降低能量,构成了超导的基态。而电子对的能隙随即为实验所证实,不久戈科夫又从微观理论导出了京茨堡-朗道方程,使BCS理论的正确性得到了确认。由于超导微观理论长期悬而不决,屡攻不克,很自然地有人将BCS理论的问世比拟于珠穆朗玛峰的被征服。
在玻色液体中若有一个宏观的被占的动量态,就规定了一个特殊的参考系,从而破坏了伽利略不变性。在量子力学中,伽利略不变性是与粒子的波函数有任意的位相因子相关联的。这类规范对称性的破缺,造成了4He的超流态。超流现象首先为Kapitza所发现,而其理论则由朗道与费因曼所建立[23]。一般情况下3He是费米液体。七十年代初Osheroff,Richardson与Lee发现在极低温条件下(低于2 mK)3He 也出现超流态。和超导相似,这也涉及费米粒子的配对问题。但超导是1s粒子态的配对,而3He超流是3p态粒子的配对,后者显然要复杂得多[24,25]。3He超流体是各向异性的量子液体,存在不止一种有序相,其序参量由两个单位矢量来描述,而且粒子之间存在磁偶极相互作用,因而对磁场有一定的响应。正因为其物理效应极其丰富,所以当3He超流被发现后,就有人预言,由此将会引出1000篇博士论文。至于超导体中是否有3p态配对的效应,也有所设想,但尚未证实。
在除了磁有序结构和超导以外,金属中还可能存在其他的由于多粒子相互作用所造成的基态。维格纳早就设想过,金属中电子按点阵排列的一种基态,称为维格纳点阵[26]。奥佛好塞提出自旋密度波(SDW)和电荷密度波(CDW)这两种基态[27,28]。所谓自旋密度波,就是每一种自旋的电子密度具有周期性的空间变化,但两种自旋的变化位相相反,保持总的电荷密度均匀。也可能两种自旋的电子密度变化保持相同的位相,这样就不出现净的自旋,而出现电荷密度的空间调制。实验观测到金属铬的基态存在自旋密度波,而在许多准二维的层状结构和准一维的链状结构的材料中,也观测到电荷密度波和自旋密度波。至于三维维格纳晶格是否存在,迄今尚未确证。但在浮沾于液氦表面的电子体系中,确实观察到二维的维格纳晶格[29]。
不同类型的基态,有的显然是可以共存的,例如晶格与铁磁性,晶格与超导性等;有的则表现为相互竞争,彼此排斥,例如超导性与铁磁性,电荷密度与超导性等。近年来,在一些含稀土的三元超导体(如ErRb4B48,HoMo6S8)中观测到重入型的超导性,即存在两个Tc,在上Tc,由顺磁相转变为超导相,在下Tc又由超导相转变为铁磁相。而下Tc表现为一类相变,存在超导相与铁磁相共存的温度区间。这种反常的超导相与铁磁相共存现象,引起了物理学家的兴趣。其共存的形式也是一个很有趣的问题[30]。中子衍射的结果表明磁矩的排列是有序的,超导体将排斥均匀的磁场,但却可允许作周期性调制的自旋,观测到的调制周期约为100埃,取决于两个对立的因素相妥协的结果。通常的磁有序结构的根源都是交换力造成的自旋耦合,而这里非常特殊的磁有序结构却是由于纯电磁力造成自旋耦合的结果。
是否还有其他尚未被发现的基态呢?回答也是肯定的。因为有许多基态,如3He超流,电荷密度波与自旋密度波,发现很迟,显然不可能就到此为止的,许多问题尚有待于进一步的探索。
04元激发
基态一般是体系在T=0的状态。因而要描述一个体系的具体物理行为,不仅要了解其基态,也需要了解其激发态。元激发在其中起了极为关键的作用。元激发的概念几乎是不知不觉地逐渐成长起来的,很难指出其创始人。使之系统化和普遍化,从而为人所周知,要数朗道四十年代的工作。最早的应用也许可溯源于德拜的比热理论(声子概念的雏形)。
安德森论述了在元激发概念的背后蕴含着两种想法[31]∶其一为基态的总能量往往并不直接影响到体系的物理行为,物理上要紧的是一些较低的温度或微弱的外场所激发的低激发态。例如半导体与金属的行为往往取决于在电场中运动的载流子,而固体的弹性或热性质则决定于少量的格波,即声子。其二是这些低激发态和其他态相比显然比较简单,可用清楚的物理概念和严格的数学 *** 来描述。这样,引入了元激发,而每个元激发具有量子化的能量和准动量,将使一个复杂的多体问题简化为接近于理想气体的粒子体系。
元激发大体可以分为两类[32]∶一类为单粒子激发或可称为“准粒子”,因为它们和用哈特里-福克近似的单电子波函数描述的粒子相类似,并和它们的体系中的个别粒子具有相同的互易律和电荷,通常它们是费米子;另外一类元激发为集体激发,主要表现为序参量在空间和时间范围内的微量涨落,一般是玻色子。
作为集体激发最早的例子是晶格振动的格波,即声子;和对应于磁序涨落的自旋波量子(磁振子)。在晶格中可以同时激发任意个相同的声子。换言之,处于声子的量子态中的声子数量是任意的,这意味着声子是玻色子。声子气体遵循玻色统计,在给定的声子态中的声子平均数,在热平衡时由普朗克函数来表示。我们也可以用声子按其量子态的某种非平衡分布来描述固体的某种非平衡状态。在上述情况中,相互作用力是短程的,随波长增大,或波矢k→0,元激发的频率亦趋于零。这种元激发相当于零质量的粒子,可以借用粒子物理的术语,叫做戈德斯通玻色子。
至于电子-电子互作用的体系,可以用金属中的电子为例。价电子在离子实的正电荷背景上运动,在宏观尺度上保持电中性。由于价电子易动,因而体系在微观尺度上必然存在着电子密度的起伏,但由于长程库仑势的作用,使局域的密度起伏也将和整个体系中电子的运动耦合在一起,产生等离子体的集体振荡。这种等离子体振荡的经典理论早就为朗缪尔与Tonks (1924)所给出,而玻姆与Pines (1955)则给出其量子理论对应于金属中等离子体振荡的元激发,被称为等离激元(pla *** on)。当k→0,等离激元的频率不等于零,而能量一般为5—30 eV。因而在这种场合,它不具有零质量的粒子。借用粒子物理的术语,这相当于Higgs玻色子。与电子气的振荡密切联系着的是屏蔽效应。库仑作用使得电子排开邻近的电子,在每个电子周围形成一个正电荷的屏蔽壳,随着激发它的电子运动。电子与屏蔽电荷加在一起构成了准电子。这是一种费米型的元激发,它们的数目与电子数一致,并且服从费米统计。在这里我们可以理解,在单电子近似的能带理论中,将电子气视为没有相互作用的粒子的 *** ,实质上是准电子的 *** 。也就是说,单电子近似还是建立在相互作用的多体物理的基础上的。
下面讨论固体电介质的电子能谱中的元激发。如果将电子从价带通过能隙激发到导带上去,这样出现了两个独立地传播着的电子和空穴,这也可以看为费米型的元激发。电子与空穴间存在库仑相互作用,可能构成束缚的电子-空穴对-激子,这是玻色型的元激发。激子的光谱具有和氢光谱相似的性质,因而有关激子的实验证据是在晶体光谱中获得的。在电介质中,电子与晶格振动的相互作用使得电子位置附近的晶格发生畸变。这样,一个电子同它所引起的晶格畸变一起,构成了极化子这一元激发。
黄昆于1951年首先讨论电磁波和晶格振动相耦合的效应[33]。特别是当光子频率ω=kc与横光学模声子的频率。ωt(~1013秒-1)相近时,两者耦合甚强,使其色散曲线发生很大的变化,形成光子-横光学模声子的耦合模式,其量子称为极化激元,这是离子晶体中的一种复合的元激发。六十年代,激光技术发展以后,观测到了多种极化激元(包括光子-声子或光子-激子相耦合的)以及表面极化激元。各种类型元激发的发现和阐明的过程尚在继续进行。正如M. Balkanski曾说过,在粒子物理领域中一个个基本粒子在被人们发现,而在凝聚态物理领域中一个个元激发在被人们发现。
在低浓度下,元激发的 *** 可以视为无相互作用的理想气体,这使理论的处理极为简便。但在高浓度下,情况又有不同。例如,在低温下利用高强度激光的照射,可以在锗晶体中产生高浓度的激子,形成激子分子和电子-空穴液滴。后者是在激子浓度达到1017厘米-3量级后的产物,原来是中性玻色子转变为由费米子电子和空穴所构成的等离子体,具有金属导体的特征。电子-空穴液滴这种新型的量子体系,具有一系列特异的性质,它的相图和凝聚过程都为人们所注意研究。高浓度元激发体系的研究构成凝聚态物理的一个新领域,其进一步的发展引人注目。
05缺 陷
集体性的元激发对应于有序结构非局域性的微扰,如果有序结构遭到严重的破坏。这样,导致在某些局域内序参量会发生突变,甚至具有奇异性(singularity),这些序参量为奇异性的区域对应于缺陷[34]。实际的例子为晶体中的点缺陷如空位与填隙原子;作为线缺陷的有晶体中的位错,超导体和超流体中的量子涡旋线,作为面缺陷的有晶体中的层错与反相畴界,铁磁体中的磁畴界和铁电体中的电畴界。有些缺陷和材料的广义刚度的破坏或建立有密切关系[5],因而缺陷往往是控制材料的某些技术性能的关键因素。例如,磁畴壁在铁磁体的磁化或去磁过程之中;位错在晶体的屈服或强化过程之中。
面缺陷最容易被人观测,因而铁磁体的磁畴和畴壁的存在早已确认。朗道与利夫希茨于三十年代中就提出了唯象的磁畴理论[1],可用以说明磁化过程,这是最早确立的缺陷理论。至于线缺陷的问题,一般要困难得多。理论的提出到确认往往要经过极其迂回曲折的坎坷历程。范性形变的位错理论就是一个突出的例子[35]。1914年C. G. 达尔文提出了 X 射线动力学衍射理论后,就和晶体衍射强度的实验数据进行对比,发现多数实际晶体是不完整的,但无法判明缺陷的具体性质。二十年代中对于金属单晶体拉伸的研究表明,金属范性形变的主要方式是滑移。Frenkel对金属滑移的理论强度进行了估计,表明它比实际强度要大约千倍。这就导致了科学家去设想一些容易滑移的缺陷组态。到1934年G. I. 泰勒明确地提出了位错这一组态,说明它与滑移与硬化过程的联系,奠定了位错理论的基础,但是科学界还是将信将疑。到1949年F. C. 夫兰克提出螺位错催化晶体生长理论,得到生长晶体表面的蜷线台阶图样的证实,才使位错得到比较直接的实际证据。到1956年P. B. Hirsch 等在电子显微镜薄膜透射观测中直接看到了运动位错,并拍摄成了电影,才使反对者偃旗息鼓。但如果翻阅一下古老科学文献,早在十九世纪就已经有位错蚀斑的图片,三十年代中也得出生长蜷线和缀饰位错线的照片,但由于缺乏理论指导,视而不见,失之交臂。二类超导体的量子涡旋线理论也有类似的命运[36,37]。三十年代后期,苏联的舒勃尼科夫研究二类超导体磁化过程,明确了一些实验规律。但这项工作在苏联以外知者甚少。1952年阿布里科索夫得到京茨堡-朗道方程的量子涡旋线阵列解来解释这一现象,由于导师朗道不甚同意,一直延至1957年方始发表。但发表以后还没有引起人们注意。直到六十年代贝尔实验室的科学家制出可以负载电流并产生强磁场的硬超导体Nb3Sn 以后,才引起科学家试图来解释这一奇特的现象,P. Goodman才发现阿布里科索夫的量子涡旋线的理论已经基本解决了这个问题。1964年中子衍射的实验证实了涡旋线列阵的存在。到1966年利用铁粉缀饰,对涡旋线点阵进行了直接观测。
应该指出,在硬铁磁体、硬超导体和高强度材料之间有其物理上的共同之处∶每一种情况下广义刚度的被破坏,是和某一种特定的缺陷(磁畴界、量子涡旋线、位错)的运动相联系在一起的。因而要阻滞这种缺陷的运动也多半采用钉扎效应。结果,这三类材料在显微组织上也有共同之处,强烈的冷加工,弥散的第二相和细微的晶粒。当然也还可能有另一条途径,就是将缺陷消除干净,如无位错的晶须和单磁畴的超细微粉。
由于缺陷物理学的发展道路比较特殊,不容易看清楚它和凝聚态物理学其他部分的联系。但近年来这种情况已经有所改变。首先,缺陷的拓扑理论的建立,表明它是凝聚态介质中的具有共性的问题[34]。1977 年 Toulouse 与 Klemen 和 Volovik 与 Mineev 相互独立地提出缺陷分类的拓扑学理论。在一种有序介质中可能存在的拓扑学上稳定的缺陷,取决于空间的维数和序参量的分量数。这种理论一方面对于凝聚态中已知的某些缺陷给予统一的分类和说明;同时也对于某些复杂有序介质(如液晶,3He超流体等)中可能存在的缺陷类型进行了预测和澄清,这些问题往往是很难从直观上作出判断的。
另一个和缺陷物理有关的基本理论问题就是孤立子(soliton)的理论[38,39]。早在1884年J. Scott-Russell在《关于波的报告》一文中报道了他在1838年目睹运河中孤立波传播的情况。这种孤立波实际上是Korteweg-de Vries(KdV)方程的一种解,后来发现其他的非线性微分方程,如 sine-戈登方程(即克莱因-戈登方程中用正弦项取代线性项)等,也具有孤立波的解。这是一种局域性的解,随着时间的演变可以保持其波形,而且两个孤立波碰撞之后,可以仍然保持其等同性,具有类似粒子的某些性质,因而被称为孤立子。现代的孤立子理论主要是在二十世纪六十年代发展起来的,首先在计算机模拟实验中取得了突破。但是晶体缺陷理论,更早地就引入了孤立子解。1938年Frenkel与Kontarova的位错模型就是建立在sine-戈登方程的孤立子解的基础上的[35],又如Seeger用的解释Bordoni内耗峰的位错弦线模型,将 sine-戈登方程孤立子解理解为位错的弯结(kink)。看来缺陷理论与孤立子理论间存在某种默契,并不是偶然的。缺陷的问题归根结底是一个非线性的问题,其完全描述必然要用非线性方程,而缺陷本身是局域的,而且随时间演变能保持其等同性,而孤立子正好给出这种特征的最简单的数学描述。但是对这类非线性的激发给出统计的描述,要比线性的元激发困难得多。Krumhansl与施里弗提出了孤立子的动态畴界模型[40],发展了初步的统计理论。
06相变与突变
在凝聚态物理中一个引人注目的重要课题,就是相变[41,42]。相变的形式是千变万化的。有的涉及结构的改变,如气体的凝聚,液体的凝固,以至于不同结构的固相间的转化;有的涉及特定物理性能的跃变,如顺磁态转化为铁磁态,正常态转化为超导态等。人们将相变划分为两类∶在一类相变中,有明显差异的两相共存于相变点,固-液相变就是明显的例子;在二类相变中,在相变点上两相合二而一,顺磁-铁磁和正常-超导相变属于这一类。这样的相变点被称为临界点。在同一种相变中,可以在不同条件下分别表现为一类和二类,液-气相变在一般情形下属一类,但在特定温度和压强下可能出现临界点,此时气体与液体的差别完全消除。临界点附近出现一些很触目的现象,如临界乳光,也牵涉到一系列物性的异常。临界现象的研究始于十九世纪的T. Andrews,他研究了气-液相变的临界点。后来吉布斯探讨了相平衡的热力学;到十九世纪末,范德瓦耳斯在他的实在气体状态方程的基础上建立了气-液相变的唯象理论,开创了相变理论的先河。现代相变理论的奠基人是朗道。他于1937年发表的二类相变理论,据他自述,是毕生理论工作中最精心之作。他强调了相变中对称性的重要性,认为对称性是不可能缓慢改变的,在或不在,不容模棱两可。这个论述如此重要,安德森称之为固休物理的第一定理。他首先引入序参量来标记破缺的对称性。在相变点附近,将体系的自由能展开为序参量的幂级数,再由对称性的考虑消去奇次项并作适当的切断。在对称相自由能的极小值对应于序参量为零处,在非对称相自由能的极小值对应于序参量不为零处。在相变点以下,自由能曲线的极大值在序参量为零处,而另一极小值在不为零处。朗道理论是唯象的,数学表述简明而物理内容丰富,在粗线条地说明相变的基本行为上取得很大的成功。它也被推广到其他的领域,例如P. G. de Gennes 考虑自由能级数的三次项,在处理液晶的一类相变问题很有成效;Mc-Millan 则用于建立非公度相变(非公度相是指调制结构的周期与晶格周期不可通约)的理论。可以这么说,对于新型相变的研究,往往是从推广朗道理论开始的。
为了解释相变,也提出一些微观的统计模型∶伊辛模型就是一个例子,它只考虑晶格座位上存在两种状态,正或反的自旋。可用以模拟铁磁相变或固溶体有序-无序相变。在伊辛模型中若采用平均场近似,即认为作用某一自旋的有效哈密顿量仅取决于长程序参量,和座位近邻排列的细节(近程序)无关,即可得出和朗道理论相同的临界行为。但是严格解出伊辛模型(L. Onsager,于1944年获得二维伊辛模型的严格解,后来有人求出三维伊辛模型的级数解)的结果却和朗道理论并不一致。
六十年代以后对于临界现象进行了大量研究,细致地测定了各种体系的临界指数
(这里Φ表示测定的物理量,ε=
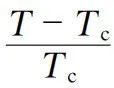
表示和临界点的偏离),并且总结出一些规律。一是普适性,临界指数与体系的具体结构无关,决定的因素是空间的维数及序参量的分量数。另一是标度律,即临界指数与T-Tc的标度无关,而且不同物理量的临界指数并不是相互独立的,需要满足一些等式和不等式的关系。这样,临界现象的行为显然和朗道的经典理论背离,其根源在于临界点附近涨落的相干长度已经达到了宏观尺寸,而经典理论只考虑微小的涨落。为了处理这种大尺度的涨落,显然需要发展新的理论 *** 。I. Kadanoff 提出将晶格划分为等同尺寸的块区,每一块区内可以求出平均自旋而近邻块区间自旋的相互作用哈密顿量与相邻座位自旋的相互作用哈密顿量相同。这样,可以继续做出更大的超块区,直到超块区的尺寸接近相干长度为止。提出了相关函数和相关长度也是与标度无关的假设。K. G. 威尔逊在此基础上发展了重整化群的理论来处理这个问题[43],在临界点的有效哈密顿将是重整化群的一固定点。从而提供了处理临界现象的有效理论 *** ,计算的结果可以全面地说明普适性与标度律。并且在临界点附近涨落的图像也是与标度无关的,不论是在微观水平上来看或是在相关长度的尺度上来看,两者的图像是相似的,重整化群就成为描述无序具有广阔频谱(从微观的到宏观的波长)的体系的自然的数学语言,在其他的物理领域中也有广泛的应用。
在固态中结构相变的一个重要问题涉及晶格变化的原子图像。特别是位移型的结构相变(有一些重要铁电体如钙钛矿型的 BaTiO3就属于这种类型)可以归结为原子的少量位移。早在1940年喇曼等在研究石英的α-β相变中,就观测到一个光频声子的频率变软。1949年Fröhlich指出钙钛矿型的铁电体,当最低光频模式的频率趋于零,静态的介电常数将趋于无限大。但铁电相变的软模理论到1959年才为Cochran与安德森全面建立起来[44]。这样,晶格振动就和结构相变联系起来了。位移型相变中静态位移可以视作光频声子软化(频率趋于零)的结果。随后对软模理论与实验研究都有很大的进展。实验研究证实了软模理论的基本环节,也发现了一些新的现象。例如,有一些晶体(如SrTiO3)在接近相变点,模式并不如软模理论所预言那样趋于零,而是出现以ω=0为中心的峰宽很窄的中心峰。关于中心峰的物理本质有不少解释∶有人认为可能是杂质或点缺陷的效应,也有人认为是微畴结构的结果,目前尚无定论。又如相变与非线性激发的耦合问题,也是一个受到重视的问题。肖克莱于1953年就提出晶体的熔化对应于大量位错产生的设想。近年来,计算机模拟实验观测还在探讨这方面的问题。但是理论上更引人注目的是有关二维相变的研究。过去的理论认为二维材料,不可能有长程序,因而排除了二维相变的可能性。1974年 Kosterlitz 与 Thouless 提出拓扑长程序的设想,即大量的位错配对或涡旋线配对相当于低温的有序相,在一定温度,配对的松解,即相当于二维的相变点[45]。近年来,在超流薄膜中观测到超流态-正常态的相变,基本符合拓扑长程序相变的理论预期。而有关二维晶体熔化问题,却尚无肯定的理论。最近在液氦表面二维电子晶格熔化的实验观察,表明确有位错介入相变的现象。总之,有关二维拓扑长程序的相变问题已成为当前统计物理极为活跃的领域。
与相变很相似的是非平衡态的突变现象。相变是从一种热力学的平衡态转变到另一种平衡态,而突变则是远离平衡态的失稳;相变牵涉到材料的微观对称性的变化,而在突变中材料的微观对称性没有改变,只出现宏观的有序结构,Prigogine 称之为耗散结构[46]。可以用液体的Benard失稳为例来说明突变现象。考虑一层液体,底部温度高于面部温度,造成下面密度比上面低,因而头重脚轻,蕴涵着导致失稳的因素。当温度梯度提高后,使瑞利数达到临界值,就产生失稳,形成一系列的对流包。Benard失稳的经典理论是由瑞利给出的,在Chandrasekhar的书中有详尽的推导和讨论,这是在经典流体力学的框架中给出的[47]。近年来,Prigogine从非平衡热力学的观点讨论了这类现象的普遍性,并给出了普适性的失稳判据[46];而Haken则强调了统计性这一侧面,建立非线性的随机演化方程,引入序参量,得到了类似于京茨堡-朗道方程的结果[48]。这类失稳现象也有类似于相变的标度律,并且在化学和生物学的过程中普遍存在,因而受到了重视。数学家R. Thom 则从微分拓扑学的奇点分类出发,创建了突变论(catastrophe theory)[49],理论的框架更加普遍化,包括了平衡态的相变和非平衡态的失稳。问题在于如何填补理论框架与物理问题之间的中间环节。
在产生Benard失稳后,如果继续增大瑞利数,将导致新的失稳,由于逐级失稳的增长,最终趋向湍流。这种从失稳通向湍流的道路早在1941年朗道就提出过理论设想。但他所设想的频谱关系(即频率愈来愈高而且是不可通约的)却和事实不符。七十年代初N. Metropolis 等提出非线性系统经过逐次周期加倍,最后达到周期为无限大,使体系处于完全的混沌态(chaos)的另一途径。1979年M. Feigenbaum发现非线性体系倍周期过程的定量规律,和相变的标度律很类似,存在一些普适性的常数,如δ=4.669,α=2.503,这些结论已在Benard系统中得到证实,而且在许多其他体系中发现了类似的倍周期导致混沌态的现象。当然,通向混沌的道路可能不止一条,理论和实验的探讨正在蓬勃开展[50]。这样,为 E. Montroll 称为“经典物理学最后的疑谜”的湍流问题的物理本质的理解开始有一些眉目。从相变,非平衡态的突变以及非线性体系的混沌态等方面研究的进展来看,K. G. 威尔逊所说的八十年代将为经典物理学取得重大进展的时期是不无道理的,而且其影响所及也远远超出物理学的范围。
07部分有序体系及无序体系
传统的固体物理所研究的对象是具有三维周期结构的晶体,破缺的平移对称性是解决问题的关键。但是许多实际的体系,这种严格的平移不变性往往遭到破坏。因而近年来人们愈来愈多地注意研究这些部分有序以至于完全无序的体系[51]。
严格的晶格平移对称性只可能在无限大的晶体中才能实现,由于晶格周期比通常晶体尺寸小七到八个数量级,因此常常忽略了晶体的尺寸的限制,将它近似地看为无限大。但晶体的表面显然就不能够这样看了。由于一个方向周期结构的截断,造成了表面层内结构的异常(弛豫与重构)以及表面所特有的能谱与元激发[52]。很显然,表面物理这一新的分支学科的建立是和超高真空技术的进展以及一系列研究清洁表面的结构与能谱的仪器(如低能衍射仪,俄歇谱仪,光电子谱仪等)的问世密切相关的。这样,就从过去无从触及的清洁表面上取得了第一手的资料,对这些资料的探讨和阐明,构成了当今表面物理的主流。但是值得注意,和气体或液体相接触的实际表面或固体中的界面问题,具有重要的实际意义,如何从基本的角度来探测和理解这类表面,目前已经有了一些苗头,显然会得到进一步的开拓。和表面密切相关的是薄膜,它是制造微电子器件的基质,对它的基础性的了解具有重要的技术意义。如果晶体在三个方向尺度都很小,就是微粒,具有特殊的物理性能和富有潜在的技术应用的可能性。在亚微米量级的微粒,具有特殊的光谱性能可资利用;而在十埃量级的微粒则具有特殊的电子性能。很有意义的是微粒的电子理论可以采取两种完全不同的处理 *** [53]∶一是从无限大晶体的能量理论出发,加上量子尺寸效应的修正;另一是从量子化学理论出发,逐步扩大原子簇的尺寸。另外Kubo提出的微粒统计理论得出一些很有意义的推论,如随着总电子数增长,交替出现抗磁性和顺磁性的奇偶效应,也尚有待实验的证实。有人称微粒物理为原子分子物理与固体物理之间的残缺环节(missing link)是颇有见地的。同样,不容忽视的是微粒的研究,将对催化这一重大技术问题提供有用的信息。
低维体系原来是理论物理学家做练习的场地。由于比较简单容易建立确切的数学模型,因而希望通过它来帮助我们理解具有现实意义的三维体系。但是近十年来情况已经大为改观,出现了一系列准二维或准一维的材料,实验和理论研究都非常活跃。准二维材料有层状结构的过渡金属硫属化合物和石墨插层化合物等[54]。前者是首先发现的电荷密度波的材料,也是研究非公度相变的典型材料;后者可以通过不同的插层来改变其电子结构。这些不仅是在基础研究中很有兴趣的材料,在应用上也有一定的前景,例如石墨插层化合物的电导率已经达到了铜的量级。准一维材料中,最令人注目的是链状分子构成的有机导体[55]。1964年W. A. Little首先提出了链状分子的有机物可能具有高温超导性的大胆设想。随后,在七十年代初出现了有关TTE-TCNQ (一种电荷转移有机盐类)在60 K 附近电导率异常大,可能是超导性的报道,轰动了学术界。后来高温超导性虽被否定,但这一类由于Peierls失稳所造成的导电异常现象,也具有新的物理内容,受到科学界的重视。在对有机导体广泛而系统的研究中,果然发现了有机超导体,例 如(TMTSF)2X(X 为PO4ClO4等),Tc只有1 K左右。TTF-TCNQ与(TMTSF)2X这两类有机材料都有一个共同的特性,即冷却到一定温度下会出现对称性的自发破缺,对应于电荷(或自旋)密度波或超导性。在长程序出现的Tc温度以上,还有一个相变的预兆区。在TTF-TCNQ的预兆区内出现Fröhlich型的电导涨落,已经得到实验的确证;而在(TMTSF)2X的Tc以上15 K范围内的一些异常现象,被解释为具有短程序的超导涨落,如能确证,将是很有意义的。最近几年聚合物聚乙炔(CH)x的导电性又成为人们注意力的焦点[56]。这是一种结构比较简单的材料,可以通过掺杂来改变其电导性,变为半导体或金属。聚乙炔具有两种不同基态结构,两种结构交接处为一畴界,相当于一孤立子,掺杂可以使孤立子带电。施里弗与Heeger 对于聚乙炔的电导给予了巧妙的理论解释∶孤立子在链上的来回运动引起电导。这种孤立子具有奇特的性质,带电时自旋为零,不带电时自旋为1/2,和正常的粒子正好相反。在一定条件下孤立子可能具有(1/3)e。的表观电荷,和基本粒子中的夸克相似。这种在理论上挺有兴趣的设想,需要进一步证实。另一方面,利用其半导体性质,已经制备了p-n结,表明在应用上是很富有潜力的。
近年来利用微电子学技术也人工制备了一些准低维的导体。例如半导体场效应管的Si-SiO2界面处反型层中的空间电荷区构成了二维电子气,对其电子结构与电导性已进行深入研究。1980年,Klietzing等发现了量子化的霍耳效应,即在强磁场中霍耳电导
,这里n为整数,e为电子电荷,h为普朗克常数。式中没有任何与材料特征有关系数,而且高度精确,可以作为精细结构常数的精密测定和电阻的绝对标准。随后,崔琪等又发现n=1/3和2/3等分数的情形。最近有人提出初步理论解释,认为这是一种新的量子液体,其元激发可以具有分数电荷,尚有待进一步的考验[57]。最近由于亚微米刻印技术的发展,可以制出线宽在0.1微米以下的反型层或金属线,从实验上直接观测准一维导体的电导性,显示出由于尺寸微小而引起的量子化效应(相当于量子力学中所谓盒中的粒子),以及低维导体电子态的局域化。这方面的理论研究也是非常活跃的。Thouless和安德森等处理了低维导体电子态的局域化的标度律。最近还有人开展了分数维结构(fractal structure)的电子态的研究。这类自相似结构也可能具有一定的现实意义。
无序体系大体上可分为两类,一类是代位无序,晶格仍然保留,但座位上原子品种或自旋状态并不是等同的。这样,就破坏了晶格的平移对称性。二元无序合金或磁无序体系属这一类。另一类是拓扑无序,晶格已不复存在,但原子在近邻范围内仍可保持一定的近程序。例如非晶硅,近邻键长和四面体配位关系仍基本保留,但四面体键组成无规网络,完全丧失周期性。又如金属玻璃,其配位数也和密积晶体相近。合金是古已有之,至今一直在技术上大量应用,但基础研究有些停滞不前;拓扑无序的玻璃也是如此,而且基础研究更为落后。六十年代初 P. Duwez 发明用急冷法制备金属玻璃后,开拓了非晶态金属这一新领域,目前在利用其力学性质和磁学性质方面已经实用化了。七十年代中,W. E. Spear用辉光放电法制出了具有掺杂性能的非晶硅,触发了对非晶态半导体研究的新 *** 。由于有可能制备出廉价太阳能电池的应用前景,使非晶半导体的研究成为固体物理的热门课题。
关于非晶态材料的结构研究,已有长期的历史,并且还在采用各种手段进行,特别是近年来发展起来的广延 X射线吸收边精细结构(EXAFS)技术。关于玻璃,三十年代W. H. Zachariason早就提出SiO2的无规网络的理论图像。这种图像颇接近于非晶态半导体的实际情况。六十年代初,J. D. Bernal提出了无规密积的液态模型,可以解释某些金属玻璃的结构。至于氧化物玻璃,最近的研究表明,实际的情况要复杂得多,可能存在有接近于微晶结构的原子簇。
早期的合金电子理论如琼斯的刚能带模型,缺乏严格的理论根据;又如莫特与J · 夫里德耳所发展的理论,只是处理了单个溶质原子对电子气的干扰,得出被称为夫里德耳振荡的电荷极化效应,与自旋的RKKY相互作用相似[58]。考虑晶格效应的合金电子理论往往采用类似于相变平均场近似的处理 *** ,用适当的宏观平均的势来代替晶格座位上的真实势。其中比较成功的是Soven等人所发展的相干势近似[59]。
处理无序体系的电子态的另一途径,是从无序体系的局域态的特点出发,设计一些无序模型,研究无序体系与有序体系电子态的差别。这方面开创性的工作始于1958年安德森的一篇题为《论无规晶格中扩散的缺席》的论文[60],其中探讨了无序体系中形成局域态的条件,后来被称为安德森局域化。安德森工作的重要意义长期未被人们理解。十年后莫脱用来建立非晶态半导体电子态的模型,认为当E<Ec|时,电子处于公有化的扩展态当E>Ec|时,则处于局域态,这里的Ec被称为迁移率边。莫脱模型在解释非晶态半导体的电导现象中取得了一定的成功,因而受到人们重视。应该说非晶态的电子理论,还是处在比较原始的阶段,需要进一步的发展。莫脱还进一步提出安德森转变的概念。例如单晶硅中掺有施主杂质磷,磷原子在晶格上作无序分布。其无序性导致一个迁移率边,只是当费米能级通过迁移率边时,才有绝缘体向金属的转变,称为安德森转变。另一种绝缘体向金属的转变,是在V2O3中观测到的,相当于载流子密度从气态到液态的突变,称为莫脱转变。与此有关还有渗流(percolation)问题,设想晶格上两种原子具有截然不同的电子性质,例如A可以构成导体而B则为非导体。因而能否存在非局域态就取决于A原子座位能否串联而成为无限大簇(infinite cluster),渗流理论就是要确定在一定成分下A原子属于无限大簇的几率,和此几率不为零的阈值。也可以进一步探讨这类结构的电导问题。总之,有人认为当前凝聚态物理学中绝缘体-金属转变取代了往昔二类相变的地位,成为尚待解决的中心课题。
拓扑无序可以和磁有序共存。只要存在近程序,磁性原子的近邻相互作用还可以保持铁磁有序性[51]。非晶态的铁磁材料已经得到技术上的应用。
另外有一种磁无序体系,称为自旋玻璃[51]。在非磁性的铜的晶格上溶有少量磁性的锰原子。锰原子作无规稀疏的分布。互作用参量Jij对距离极其敏感,结果在Ri与Rj处的自旋符号由于RKKY互作用振荡项的影响,变得可正可负。这样,每一自旋受到大量互作用效应的叠加,其有效
的大小和方向就都是无规的,造成自旋的无规分布。自旋玻璃的一个基本问题是,它是否是一个热力学的稳定相,类似于磁有序相。这个问题有一定的普遍性。在这类问题上,宏观序参量的概念遇到了困难。安德森认为这一类转变到有刚度的类似玻璃的状态,可能存在一种隐秘的微观序参量来描述体系的刚度[5]。
无序体系也包括液态。气态是以其完全无规性最先为统计理论所描述;另一极端的固态却由于其高度有序性也得到简化理论描述。而处于两者之间的液态,却是最难进行理论处理的。虽然可以有两种完全不同的道路来趋近这个问题∶一是当作稠密的气体。另一是当作无序固体的某种变体。前者是传统的液体统计理论的做法,但自从固体物理发展以后,后者也颇有成效。特别是对于那些可以采用序参量来描述的液体,例如具有超流动性的量子液体和具有空间指向序的液晶。近年来高聚合物溶液问题有了一些新的发展[61]。所谓聚合物是由长链分子所构成。每个分子由结构等同的单元所连成的。每个分子的单元数可高达104—105。早在三十年代,物理化学家 W. Kuhn 与P. J. Flory 等就发展了聚合物溶液的统计理论。近年来de Gennes指出聚合物分子的单元数很大,和临界点附近相干长度很大,本质上是相似的。这样,临界现象的普适性和标度律,也将在聚合物溶液问题中有所反映(单元的化学结构将不影响问题的普适性)。他将重整化群理论用来处理这方面的问题,取得了成功。