抽屉原理的诀窍,抽屉原理的三个公式小学
本文目录
1.抽屉原理的三个公式小学 2.抽屉原理是什么重要原理 3.抽屉原理的三个公式 原来是这样的吗 4.抽屉原理的三个公式是什么意思
抽屉原理的三个公式小学
原理1: 把多于n+1个的物体放到n个抽屉里,则至少有一个抽屉里的东西不少于两件。
第二抽屉原理
把(mn-1)个物体放入n个抽屉中,其中必有一个抽屉中至多有(m—1)个物体(例如,将3×5-1=14个物体放入5个抽屉中,则必定有一个抽屉中的物体数少于等于3-1=2)。

扩展资料
在任意的五个自然数中,是否其中必有三个数的和是3的倍数。
分析与解:根据例2的讨论,任何整数除以3的余数只能是0,1,2。现在,对于任意的五个自然数,根据抽屉原理,至少有一个抽屉里有两个或两个以上的数,于是可分下面两种情形来加以讨论。
第一种情形。有三个数在同一个抽屉里,即这三个数除以3后具有相同的余数。因为这三个数的余数之和是其中一个余数的3倍,故能被3整除,所以这三个数之和能被3整除。
第二种情形。至多有两个数在同一个抽屉里,那么每个抽屉里都有数,在每个抽屉里各取一个数,这三个数被3除的余数分别为0,1,2。因此这三个数之和能被3整除。
综上所述,在任意的五个自然数中,其中必有三个数的和是3的倍数。
参考资料来源:百度百科-抽屉原理
抽屉原理是什么重要原理
1、如果每个抽屉代表一个集合,每一个苹果就可以代表一个元素,假如有n+1或多于n+1个元素放到n个集合中去,其中必定至少有一个集合里至少有两个元素。
2、把多于n个的物体放到n个抽屉里,则至少有一个抽屉里有2个或2个以上的物体。把多于mn(m乘以n)个的物体放到n个抽屉里,则至少有一个抽屉里有m+1个或多于m+1个的物体。

抽屉原理的三个公式 原来是这样的吗
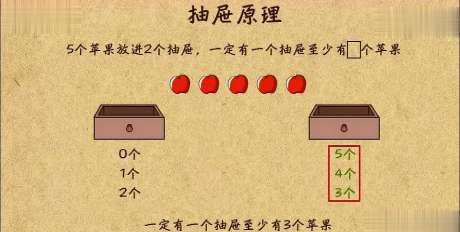
1、三个苹果放进两个抽屉,必有一个抽屉里至少有两个苹果。
2、抽屉原则的常见形式一,把n+k(k≥1)个物体以任意方式全部放入n个抽屉中,一定存在一个抽屉中至少有两个物体。
3、二,把mn+k(k≥1)个物体以任意方式全部放入n个抽屉中,一定存在一个抽屉中至少有m+1个物体。
4、三,把m1+m2+…+mn+k(k≥1)个物体以任意方式全部放入n个抽屉中,那么后在一个抽屉里至少放入了m1+1个物体,或在第二个抽屉里至少放入了m2+1个物体,……,或在第n个抽屉里至少放入了mn+1个物体四,把m个物体以任意方式全部放入n个抽屉中,有两种情况:①当n|m时(n|m表示n整除m),一定存在一个抽屉中至少放入了 个物体;②当n不能整除m时,一定存在一个抽屉中至少放入了[ ]+1个物体([x]表示不超过x的最大整数)。
抽屉原理的三个公式是什么意思
三个公式:
1、把多于n+1个的物体放到n个抽屉里,则至少有一个抽屉里的东西不少于两件。
2、把多于mn+1个的物体放到n个抽屉里,则至少有一个抽屉里有不少于m+1的物体。
3、把无穷多件物体放入n个抽屉,则至少有一个抽屉里有无穷个物体。
桌上有十个苹果,要把这十个苹果放到九个抽屉里,无论怎样放,会发现至少会有一个抽屉里面放不少于两个苹果。这一现象就是所说的“抽屉原理”。

原理1: 把多于n+1个的物体放到n个抽屉里,则至少有一个抽屉里的东西不少于两件。

抽屉原理
证明(反证法):如果每个抽屉至多只能放进一个物体,那么物体的总数至多是n×1,而不是题设的n+k(k≥1),故不可能。
原理2:把多于mn(m乘n)+1(n不为0)个的物体放到n个抽屉里,则至少有一个抽屉里有不少于(m+1)的物体。
证明(反证法):若每个抽屉至多放进m个物体,那么n个抽屉至多放进mn个物体,与题设不符,故不可能。
原理3:把无穷多件物体放入n个抽屉,则至少有一个抽屉里 有无穷个物体。
原理1 、2 、3都是第一抽屉原理的表述。
以上就是关于抽屉原理的诀窍 ,抽屉原理的三个公式小学的全部内容,以及抽屉原理的诀窍 的相关内容,希望能够帮到您。